이번에는 a와 b의 대소 관계에 상관없이 사이의 모든 정수 합 구하기를 한번 해보겠습니다. 우선 시작하기에 앞서, 1부터 10까지의 정수의 합을 구해보겠습니다.
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
이 경우의 답은 모두들 알다시피 55입니다. 이 방식을 while을 사용해서 코드화 해보자면,
int n = 10;
int i = 1;
int sum = 0;
while ( i <= 10 ) {
sum += i;
i++;
}이렇게 표현할 수 있겠습니다. 혹은 for을 사용하면,
int n = 10;
int sum = 0;
for (int i = 1; i <= 10; i++){
sum += i;
}이렇게 표현할 수 있겠습니다.
하지만, 모든 정수의 합을 이렇게 구하면 나중에 구하고자 하는 값이 커질 때 처리속도가 아무래도 많이 늦어지게 됩니다. 그래서 우리는 가우스의 덧셈 공식을 사용해보려고 합니다. 예를 들어 1부터 8 사이의 정수의 합을 구한다고 가정합시다.

1에서부터 8까지를 나열 후, 거꾸로 8부터 1까지 또 나열하여 그 수를 더합니다. 그렇게 되면 9가 8개 나오게 되겠죠. 하지만 이 식에서는 1부터 8까지를 두 번 더한게 되니 나누기 2를 해주게 되면 총 36이 나오게 됩니다.
이번에는 8이 아닌 n을 사용하여 공식화 한다면 다음과 같습니다.

이 공식이면 반복문 사용 없이 1부터 n까지의 모든 수를 구할 수 있게 되는 것이죠.
다시 원 문제로 돌아가보겠습니다. 대소 관계없이 a부터 b 사이의 모든 정수의 합을 위 공식을 사용하여 한번 만들어보겠습니다. 우선, a와 b의 대소관계를 정의해야 합니다.

위의 방식을 사용하여 a, b에 어떤 값이 들어와도 위 식을 통하여 a에는 작은값, b에는 큰 값이 들어가게 될 것입니다.
예를 들어, a를 3, b를 5라고 가정해보겠습니다.

이 결과값을 내고 싶은데 만약 가우스 식을 사용하여 이 문제를 풀게 된다면,
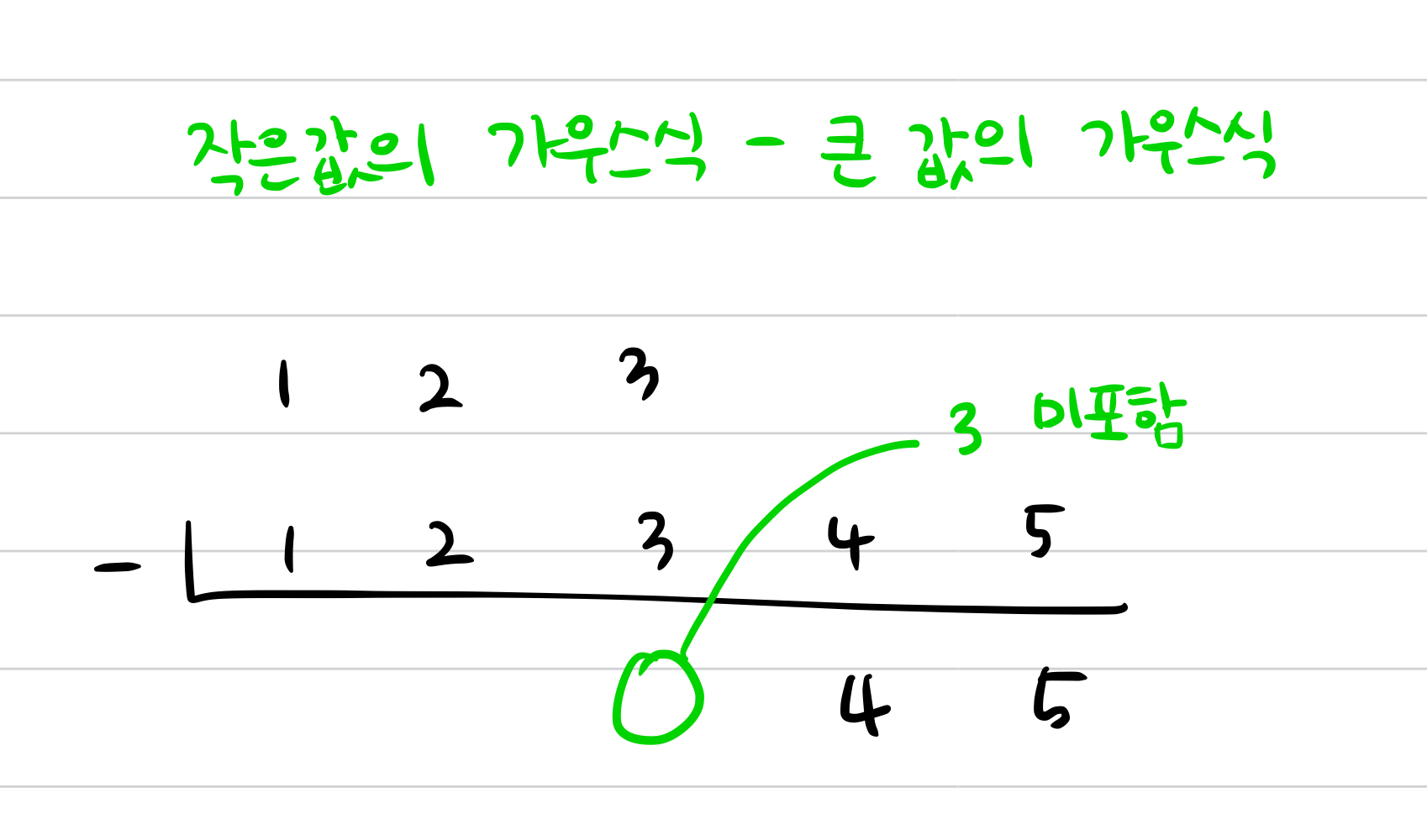
이렇게 3이 포함되지 않게 됩니다. 이럴 경우, 작은값의 가우스식에서 -1을 해주면 사이값을 포함할 수 있게 됩니다.

그럼 코드화 해보겠습니다.

코드를 이렇게 짜보았습니다. 가우스식을 함수로 재 정의 한후 불러오는 것이 효과적일 것 같습니다. 제가 임의로 만들어 본 알고리즘이라 저렇게 함수를 두번 정의하게 되었어요ㅠㅠ 공부하다보면 더 나은 방식으로 배워가겠죠?
또 이렇게 알고리즘을 공부하다보면 결과값만 보고 어디서 꼬였는지 알기 힘들때가 있죠ㅠ 그럴때는 디버깅을 사용해서 variable 안에 어떤 값이 있는지 차근차근 따라가며 수정해봤습니다. 디버깅은 우선 breaking point를 걸어주시고 위 Debug를 눌러주시면 됩니다.
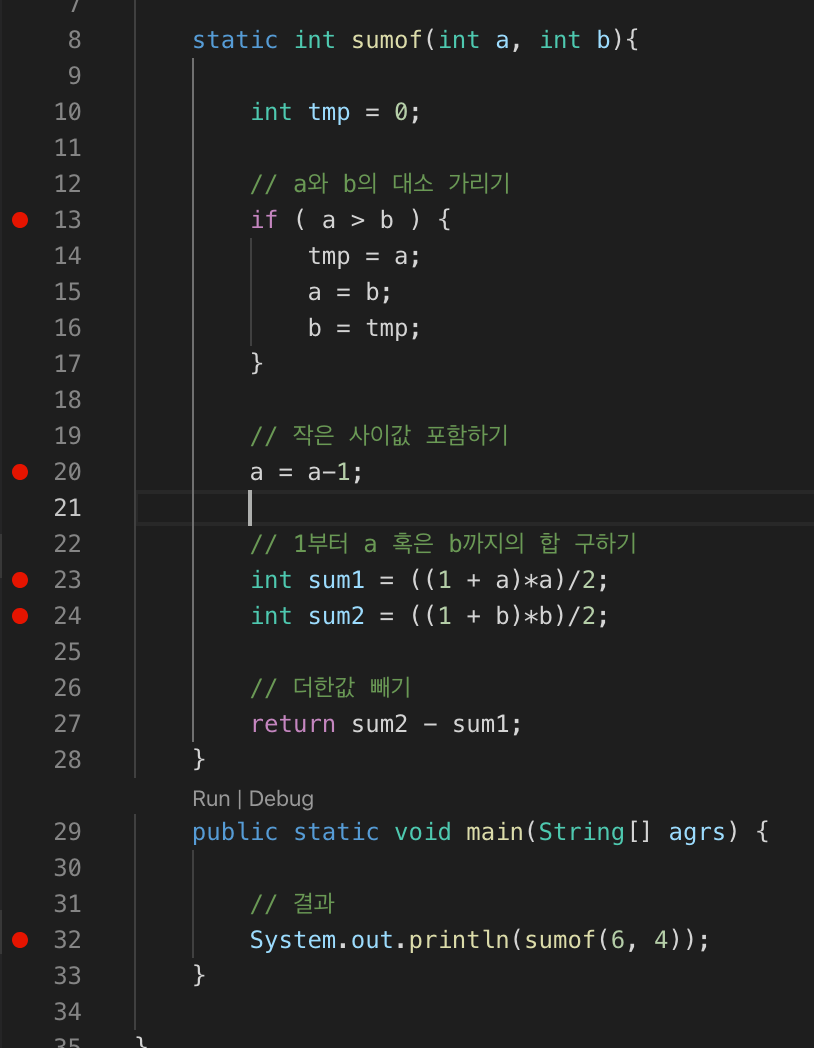
옆의 빨간 점이 break point입니다. 저 포인트에서 variable 값을 live로 확인할 수 있습니다. 아래처럼요-
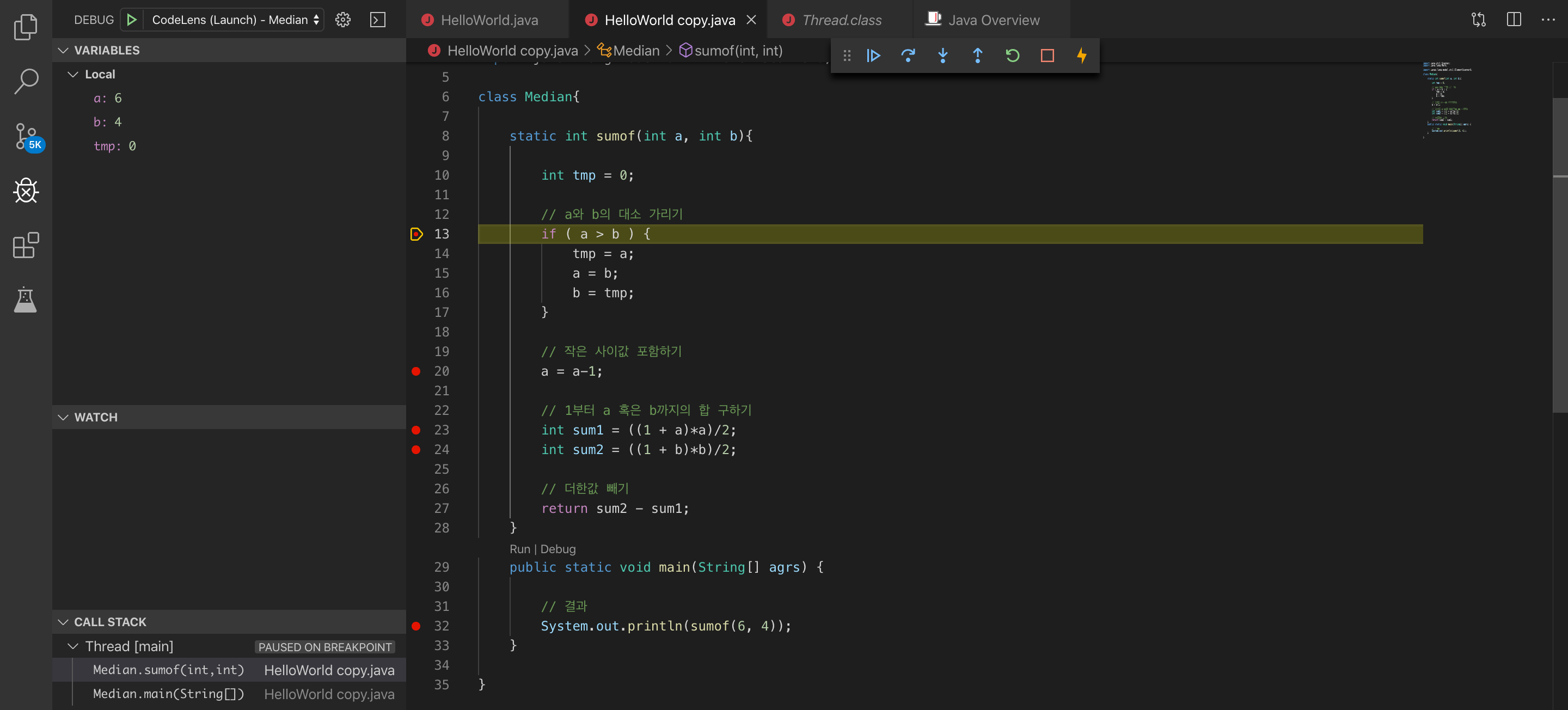
우선 6, 4가 들어갔습니다. a가 b보다 크니 if문 안에 들어가게 되겠죠.

tmp값에 6이 들어갔습니다.

if문을 빠져나오니 a와 b가 바뀐 것을 확인할 수 있습니다!

작은 사이값 포함해주고-

각각 가우스 공식을 적용해준 결과-

결과값을 15로 리턴받았습니다. 정확하죠? :)

오늘은 반복문 대신 가우스 공식을 이용해서 풀어봤습니다. 누군가에게는 아주 쉬운 알고리즘일 수 있지만 전 첫걸음이라 정속으로 밟아갈 예정입니다. 개선이 필요한 부분 혹은 오류는 잡아주세요!! 꾸준히 공부해야지 다짐하며 오늘은 여기까지! :)
'개발 기록 (~2023)' 카테고리의 다른 글
| 알고리즘) 백준 2884번 알람시계 (0) | 2020.01.14 |
|---|---|
| 알고리즘) map 함수를 사용하여 자릿수 나누기 (0) | 2020.01.14 |
| 개인프로젝트) Velog 형식의 웹사이트 개발-1 (0) | 2020.01.11 |
| 알고리즘) 세 정수 중앙값 구하기 (7) | 2020.01.08 |
| 1월 8일 주저리 (0) | 2020.01.08 |