일반 세 정수의 중앙값 구하기 알고리즘입니다. 일반 세개의 정수를 나열한다고 가정했을 때, 나올수 있는 경우의 수를 결정 트리(decision tree)로 표현한다면 아래와 같이 표현할 수 있겠습니다. 여기서 세 정수를 a, b, c로 가정하겠습니다. 여기서는 자바로 표현됩니다.
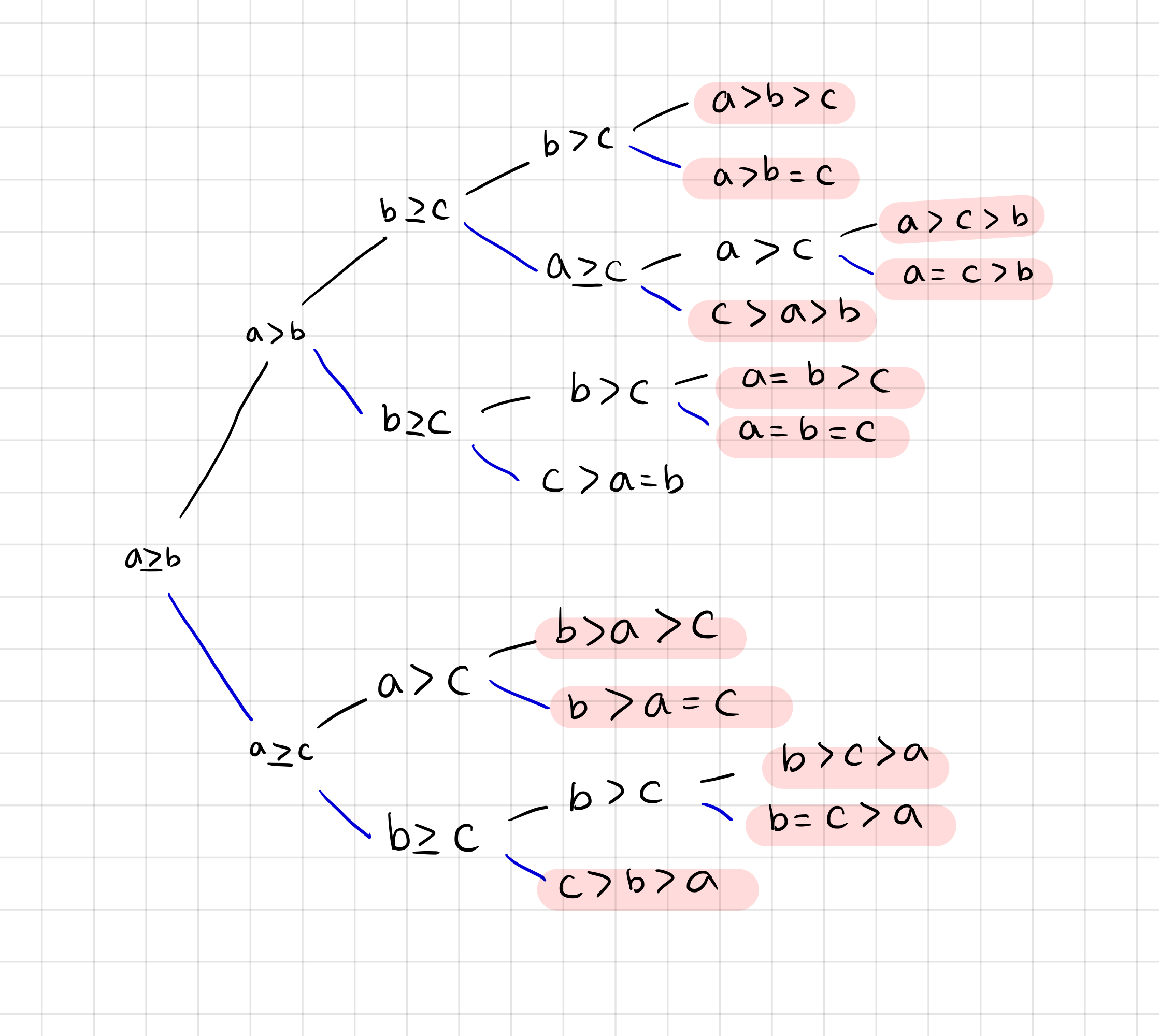
수가 같을 경우를 가정한다면 경우의 수가 더 늘어나게 되죠. 이를 살펴보겠습니다.
어차피 수가 같다고 가정하더라도, 수는 나열될 수 밖에 없습니다. a와 b가 같다고 가정해도 어차피 중앙값만 돌려받기 때문에 a b c 나 b a c인 경우 중앙값은 같게 되는 것이죠. 이럴 경우 나올수 있는 경우의 수는 여섯가지가 됩니다.

이 경우에서, c를 기준에 따라 위치시켜봅시다.
1. a가 b보다 큰 경우 (a > b)

a는 무조건 b보다 앞에 위치해야 합니다. 이런 경우에 c가 위치할 수 있는 경우의 수는 아래와 같습니다.

1번은 a b c, 2번은 a c b, 3번은 c a b가 되겠습니다.
1번의 코드화 ( a - b - c ). 중앙값이 b가 됩니다.
if (a >= b)
if (b >= c)
return b;
3번의 코드화 ( c - a - b ). 위의 코드와 이어집니다.
...
else if (c >= a)
return a;
2번의 코드화 ( a - c - b )
...
else
return c;
여기까지 해결한 경우의 수는 a b c, a c b, c a b가 되겠습니다. 아래 그림으로 지금까지의 코드를 확인해주세요.

이제 나머지를 살펴봅시다.
2. b가 a보다 큰 경우 (b>a)

여기서도 경우의 수가 세가지가 되겠습니다. 1번 b a c, 2번 b c a, 3번 c b a 이 세가지 경우를 살펴봅시다.
1번의 코드화 ( b - a - c ). 위의 코드와 이어집니다. 전제 조건은 위의 조건, a > b에 해당되지 않는, b가 a보다 큰 경우에 해당됩니다. 아래의 조건에 부합하지 않는 코드는 2번, 3번의 코드에 부합하겠죠.
...
else if (c < a)
return a;
2번의 코드화 ( b - c - a ) 역시 위의 코드와 이어집니다. 이번에는 c가 b보다 클 경우입니다.
...
else if (b > c)
return c;
3번의 코드화 ( c - b - a ).
...
else
return b;
b가 a보다 클 때의 나머지 경우의 수입니다.

위와 아래를 합쳐주면 결국 이런 결과가 나오게 됩니다.

이렇게 코드로 표현하면 모든 정수 세개 중 중앙값을 추출할 수 있겠습니다. 우리모두 알고리즘 열공!
'알고리즘' 카테고리의 다른 글
| 알고리즘) 2742 기찍 N (0) | 2020.01.17 |
|---|---|
| 알고리즘) 백준 15552번 A+B (0) | 2020.01.17 |
| 알고리즘) 백준 2884번 알람시계 (0) | 2020.01.14 |
| 알고리즘) map 함수를 사용하여 자릿수 나누기 (0) | 2020.01.14 |
| 알고리즘) a와 b의 대소 관계에 상관없이 사이의 모든 정수 합 구하기 (0) | 2020.01.13 |